Up till this point, many of our simulations have been based on "first principles." By this I mean, we take a fundamental idea about how nature works, like conservation of momentum, encode it in an equation, and try to solve that equation numerically. For wind-blown sand, the fundamental principles involved are quite complex (fluids, particles transport, particles colliding).
Often, the biggest choice someone makes in developing a model is about their expectation of how much detail is required to recapitulate the dynamics they’re interested.
For example: although we have a descriptions of the physical world which are incredibly accurate (e.g. quantum mechanics), it very rarely makes sense to start from there in developing a model. The questions of what a ’successful’ model entails (is it qualitative similarity? Do you have some quantitative standard?) and what dynamics you expect you will need to explicitly encode to recreate that phenomena are central to understanding the various approaches people take.
In looking at windblown particles, one family of approaches assumes that we can largely ignore the detailed physics of what is going on, and that what’s important is to understand the effects in aggregate. i.e. “Net, sand is moving away from this patch and into this other patch.” At the other end of the spectrum, there are modes which try to simulate every aspect of the environment in detail. For example, these models might model the detailed flow and turbulence of wind, the interaction between the wind and the sand, etc.
Along similar lines, when simulating complex phenomena, there are often aspects which appear to be essentially random. Some approaches to modeling these phenomena embrace this randomness and simulate particle-level dynamics which incorporate a random component. These are known as stochastic models. An alternative is to look at the particles in aggregate and focus on the trends that persist independent of that randomness. For example, one approach to simulating diffusion is to make each particle take a random walk, “Brownian motion.” But, you can also zoom out and think of diffusion as an aggregate process of many random walks that tends to move from regions of high concentration to regions of low concentration.
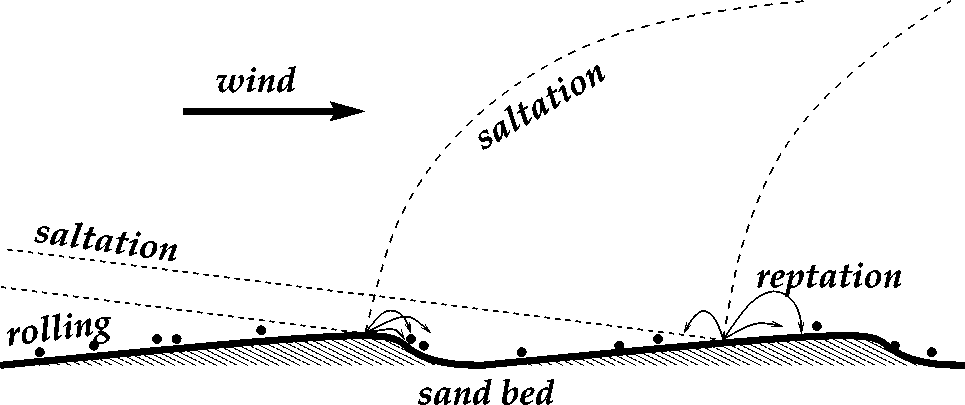
When describing dune formation (aka Aeolian processes), people typically abstract out much of the complex behavior involved (fluid motion, wind carrying particles, collisions). Instead they refer to four different processes:
-
saltation :: or less jargonly: particles jumping (in the case of desert dunes, ≈ 10\textrm{cm}) by getting kicked up by the wind. In other words, the wind blows by some sand, and occasionally, it picks up the sand and throws it some distance away.
- creep :: particles rolling around, but never leaving the ground, due to wind and/or gravity. So for example, when the ground is flat and wind is blowing over it, particles move and slide around on top of one another, even if they aren’t lifted into the air.
suspension :: particles which get carried into the air for a significant period of time (multiple timesteps).
reptation :: or less jargonly: when grains of sand which have been lifted into the air impact other grains of sand and cause them to kick up and splash small distances. These tend to travel a much shorter distance than particles which are “saltating.”
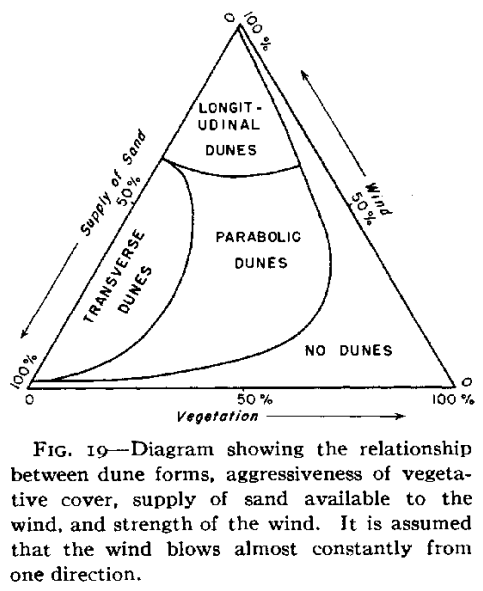
People have been working for a long time to develop a model which recreates the various qualitative and quantitative aspects of dunes. This is hard in part because there are tons of different types of dunes and sand ripples and a number of different conditions under which they develop (e.g. behind plants).
Nishimori and Tanaka created a simple model of dune formation which recreates the qualitative behavior of different types of sand dunes that people have observed over the years. A nice visual summary of this is Hack’s phase diagram
This model tries to simplify the simulation by looking at the mass behavior of sand particles, instead of thinking about each, individual one. For them, dune formation is the result of primarily two processes:
inertial or advection process :: the mass effect of particles jumping around (saltating) due to wind.
frictional or diffusion process :: essentially, random motion of sand particles due to the fact that the natural world is very rarely perfect—dune surface irregularities, erratic wind, etc.
Nishimori and Tanaka’s approach starts with a big grid (“lattice”) of cells. Each cell in the ith row and jth column has a height h(i,j). Each time step, the various heights of the cells change as sand moves between them. The cells are big enough such that the height change indicates the net movement of sand, not the movement of individual grains.
At each time step, sand moves out of each cell depending on how strong the wind is, where it is blowing, what the local slope of the sand is, and what the local slope is in the direction of the wind.
The local slope affects how likely sand is to roll downhill—the “frictional” process is essentially random motion which is weighted by the slope of the surface (so, even though the sand is moving randomly, it is more likely to move in the direction that the sand is sloping).
The slope of the sand in the direction of wind is the the central piece which creates the “inertial” or “advection” behavior. People have observed that on the windward side of sand hills (i.e. the side facing the wind), the wind velocity is much higher than on the lee side (the side facing away from the wind). This is largely because the wind running into the hill gets compressed and pushed up the side of the hill, whereas on the lee side, it spills over the top and is shielded from the wind “behind” the hill.
Part of the simplicity of this model comes from the fact that they explicitly ignore the complex dynamics of individual sand particles. The amount a sand particle jumps by is very sensitive to the shape of the sand (which is in turn determined by the amount sand particles move when carried by the wind). Despite this, by talking about the behavior of many sand particles in aggregate, our job gets a lot easier.
In particular, to accommodate Rasmussen’s observations of how local slope of the sand (in the direction of the wind) affects wind speed, they choose to make the amount a particle jumps (saltates) by (also known as the “transport length”) and the amount removed from each cell (the “height transfer”) depend on tanh of the slope. tanh is short for “hyperbolic tangent,” and the choice to use it was kind of arbitrary: we need a function which increased nonlinearly and plateaued at a low number above zero, and decreased and plateaued nonlinearly and plateaued at a low number below zero. tanh does this.
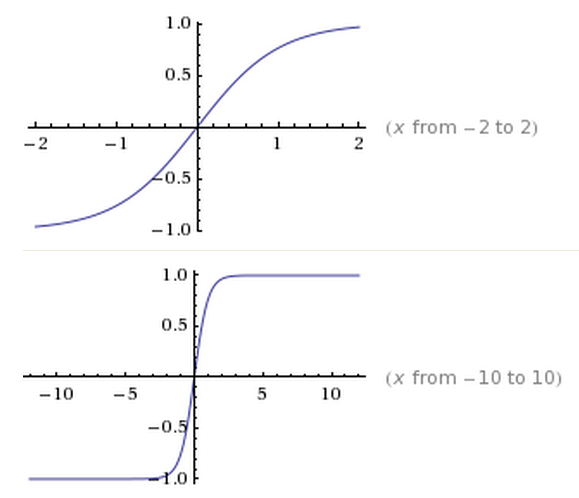
Why the relationship between windspeed and slow is nonlinear (and in particular, why the nonlinearity of tanh is a reasonable approximation) has partly to do with the compressibility of air and some facts from fluid dynamics.
There are a number of ways to refine and extend Nishimori and Tanaka’s model by taking into account other behaviors of sand we know about. Something to keep in mind is that our model focuses on modeling sand
in aggregate, so it may be easy to come up with many more refinements which may not necessarily affect the large scale behavior of the system. For example, introducing a model of turbulence is unlikely to change the large scale behavior if in effect, it is simply introducing more randomness or noise to the diffusion step. On the other hand, if you get patterned turbulence (e.g. persistent vortices), you could imagine this dramatically changing the behavior of the system.
Much of the point of this “minimal model” is that our finely-grained physics-driven understanding can sometimes make it hard to see the forest for the trees.
In short, the critical angle of repose is the steepest angle a pile of granular material can make. You may have noticed that piling loose, dry sand results in a much flatter mound than wet sand—at some point, the angle becomes too steep (and the effect of gravity too great) for the sand to avoid rolling down and falling. The size, shape, and wetness of the sand control where this critical angle is
Usually, this critical angle is between 15 deg–30 deg. Incorporating it into our model of dune formation would involve adjusting our weighting of the frictional process by slope to be more nonlinear—rather than have it simply increase with slope, we’d like it to increase nonlinearly and reach a point where at the angle of repose, sand will definitely roll.


