Researcher Profile: Nigel Goldenfeld
Nigel Goldenfeld is a professor of Physics at the University of Illinois, Urbana-Champaign who has worked on a wide-variety of fascinating topics. We have encountered his research time and time again, more than any other scientist. From his bio: “Nigel’s research explores how patterns evolve in time; examples include the growth of snowflakes, the microstructures of materials, the flow of fluids, the dynamics of geological formations, and even the spatial structure of ecosystems. Nigel’s interests in emergent and collective phenomena extend from condensed matter physics, where he has contributed to the modern understanding of high temperature superconductors, to biology, where his current work focuses on evolution and microbial ecology.”
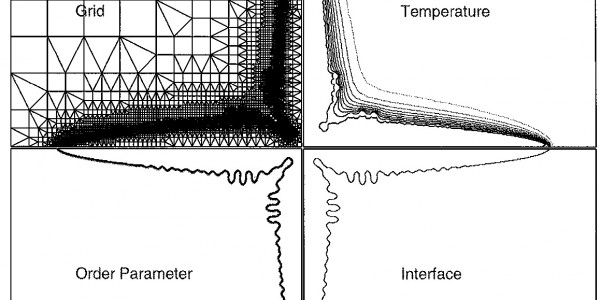
Much of his work focuses on the dynamics of solidification and crystal growth. We encountered this research recently while studying dendritic solidification and viscous fingering, which we have begun to explore here. His work spans theoretical analysis of complex dynamics and instability as well as numerical studies. I’ve specifically been looking at his work on efficient methods for simulating dendritic structures which uses adaptive mesh refinement to increase computational efficiency in phase-field models. Phase-field models are particularly attractive for the implicit representation of phase boundaries. Instead of explicitly representing geometric boundaries by surfaces or curves, which can be complex, phases are represented as a numerical field distributed in space, allowing for direct use simple simulation techniques like finite differences. He has a host of papers on other topics involving crystal dynamics that I have not yet explored.


Like Hammer, we first found Goldenfeld’s work while researching sinter terraces. He participated in physical and computation studies of the dynamics of travertine dams, building a numerical model based on both the fluid and chemical dynamics of the precipitation that leads to terrace formation, unlike Hammer’s simplified model that only looked at fluid flow.
While much of his research has focused on dynamics and pattern formation in materials, his research group applies the principles of complexity learned from this broadly with research in geology, cosmology, population dynamics, autism, ecology, genetics, and more.
His more recent work looks at complex dynamics in biological systems. It explores topics from genetics to microbial ecology. The thrust of the research is looking at the emergence and origins of life. He has a wonderful overview of this research here. It also contains a great definition of complex systems:
“Complex systems are characterized by the presence of strong fluctuations, unpredictable and nonlinear dynamics, multiple scales of space and time, and frequently some form of emergent structure (riots, herds, .). The individual components of complex systems are so tightly coupled that they cannot usefully be analyzed in isolation, rendering irrelevant traditional reductionist approaches to science, obscuring causal relationships, and distinguishing complexity from mere complication. Biological complexity, or biocomplexity, arises from the inclusion of active components, nested feedback loops, and multiple layers of system dynamics, and is relevant to numerous aspects of the biological, medical and earth sciences, including the dynamics of ecosystems, societal interactions, and the functioning of organisms.”