Puzzle pattern repair and optimization

This week I revamped the automatic post-processing of puzzle files. Previously, there was a lot of manual work that had to be done to the file before they were ready to be laser cut. Now, I’ve reduced a lot of that labor and also made it so that the puzzle pieces will be generated with much more consistent details and nubs.

The problems

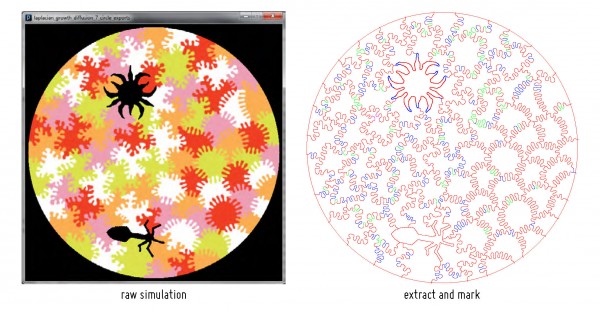
There are a number of problems that have to be found and fixed by hand. Many of these issues occur around whimsies. Some pieces are generated too small to be a usable piece. Other times pieces get merged during the simulation. This occurs when two pieces which have the same phase grow into each other during the simulation. This can occur because the simulation employs an optimization of only having 5 phases rather than each piece being its own phase. Some areas are just too thin.

Fixing overview

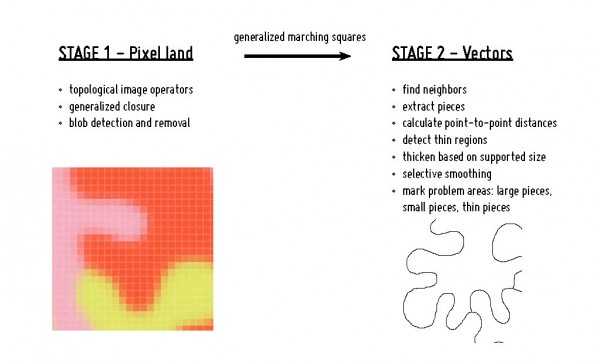
Fixing occurs in two stages. The first part occurs in pixels space before the boundaries have been extracted. This part hasn’t changed. The second stage works in vector space, once everything is represented as polylines. To get from the first stage to the second stage we used a modified marching squares algorithm.

The difficulty

What makes the fixing tricky is that conditions that define what needs to be fixed and how are highly non-local. I cannot simply say nothing can be under X thickness. The more material a connection holds, the thicker it needs to be. Thin areas between two merged pieces need to be split, not thickened. Even thickness is a bit tricky to calculate. Additionally, there can be conflicts where thickening one area makes another too thin.

Marching squares

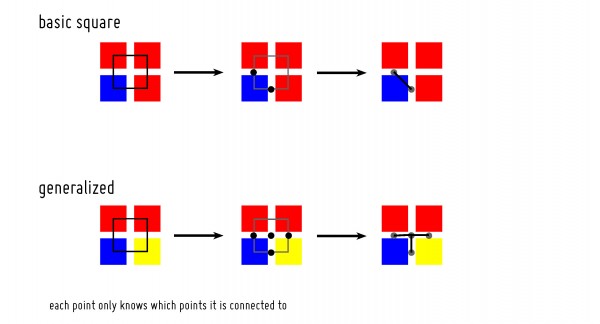
To explain the fixing procedure in detail, I’ll start at the beginning with the creation of the vector representation. The pixel representation is turned into vectors with a generalized marching squares algorithm that allows for an arbitrary number of states. During this process each point only knows which points it is connected to. There is no notion of pieces having any continuity.

Computing thickness

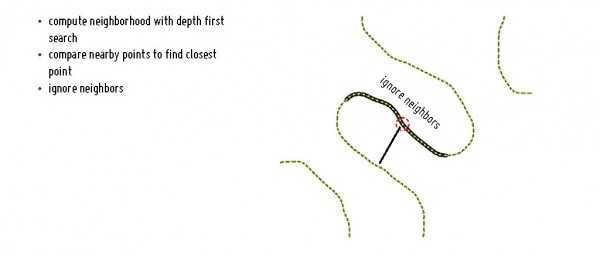
To compute the thickness of each point, I find the distance to the nearest non-degenerate point. I don’t bother to be concerned with distance to a line segment because the curves are so dense. By non-degenerate point, I mean that points that are directly next to another should not be considered for thickness computation. So for each point I compute a local neighborhood that extends out a certain distance using a depth first search of the neighbors. The points in this neighborhood are considered degenerate.

Minimum thickness computation

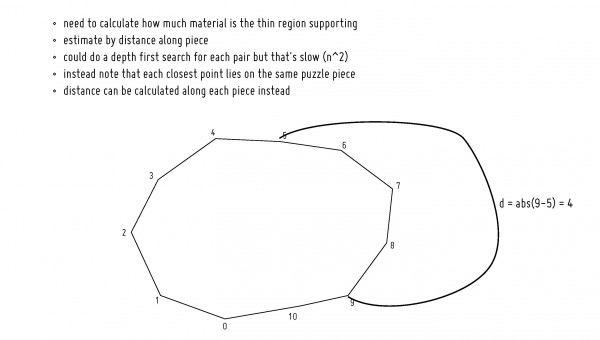
To compute how thick a connection needs to be, we need to know how much material it supports. This is estimated by the linear distance along the piece from one end of the connection to the other, rather than trying to compute the actual area. We could compute this distance with a breathe first search, but that would be expensive O(n^2).

Instead, we note that two nearest points must lie within the same piece. This way if we extract each puzzle piece and label each point in the piece with the distance along it starting at an arbitrary point, we can do a simple calculation to get the distance between any two points. It is constant time.

Extracting the pieces themselves isn’t entirely trivial. This equates to finding all minimum cycles in a graph. However, we have a clue that makes this a bit easier. Each point knows the colors of the pixels that is was generated in between, and we can tag them with this information. Because of this if you trace along an arbitrary point’s neighbors that all have the same color, you get a piece. This creates a simple linear time procedure for extracting all pieces.

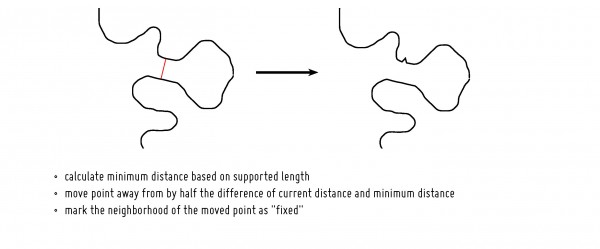
Thickening

The thin regions are thickened by simply moving a point away from the nearest point, such that it is the minimum distance calculated from the material supported. All points in the local neighborhood of moved point are then marked.

It should be noted that special consideration needs to be paid to boundary pieces, which need to treat the edge of the puzzle slightly differently.

Selective smoothing

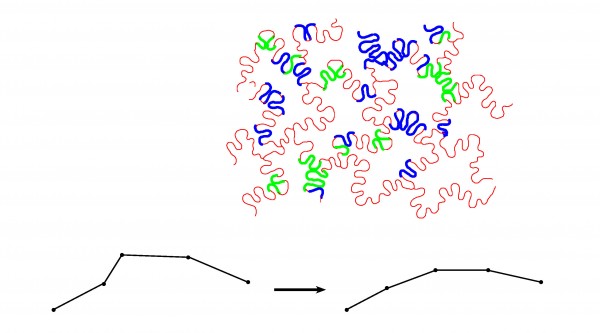
All points that have been marked by the thickening process are then smoothed with a Laplacian smoothing procedure. This alleviates any strange geometry that might arise from movement.

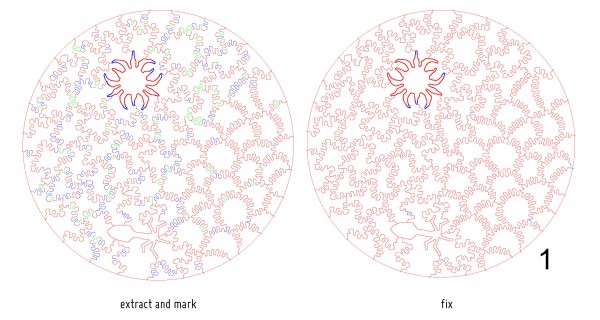
These processes of marking, thickening, and smoothing are repeated in a relaxation procedure that resolving conflicting situations when thickening one area overly thins another.

Small and merged pieces

All of these procedures only deal with thin regions. So far, there are no automatic fixes for small and merged pieces. Instead these are marked on export for manual fixing. Merged pieces are heuristically identified simply by their size, which can lead to false positives, but that is easily distinguished by a manual operator. With the pieces already extracted, marking small are large pieces is trivial.

Results

Here are the resulting files. The two marked “extract and mark” are identical and show the output of marking the pieces before they are fixed. Click on them for a larger view.