Earth and Moon Infinity Puzzles ™

Explore the Earth and Moon through our mind-bending, never-ending jigsaw puzzles. The Earth Infinity Puzzle is a map of the globe unlike any you’ve seen before. Start anywhere and see where your journey takes you. This puzzle is based on an icosahedral map projection and has the topology of a sphere. This means it has no edges, no North and South, and no fixed shape. Try to get the landmasses together or see how the oceans are connected. Make your own maps of the earth!

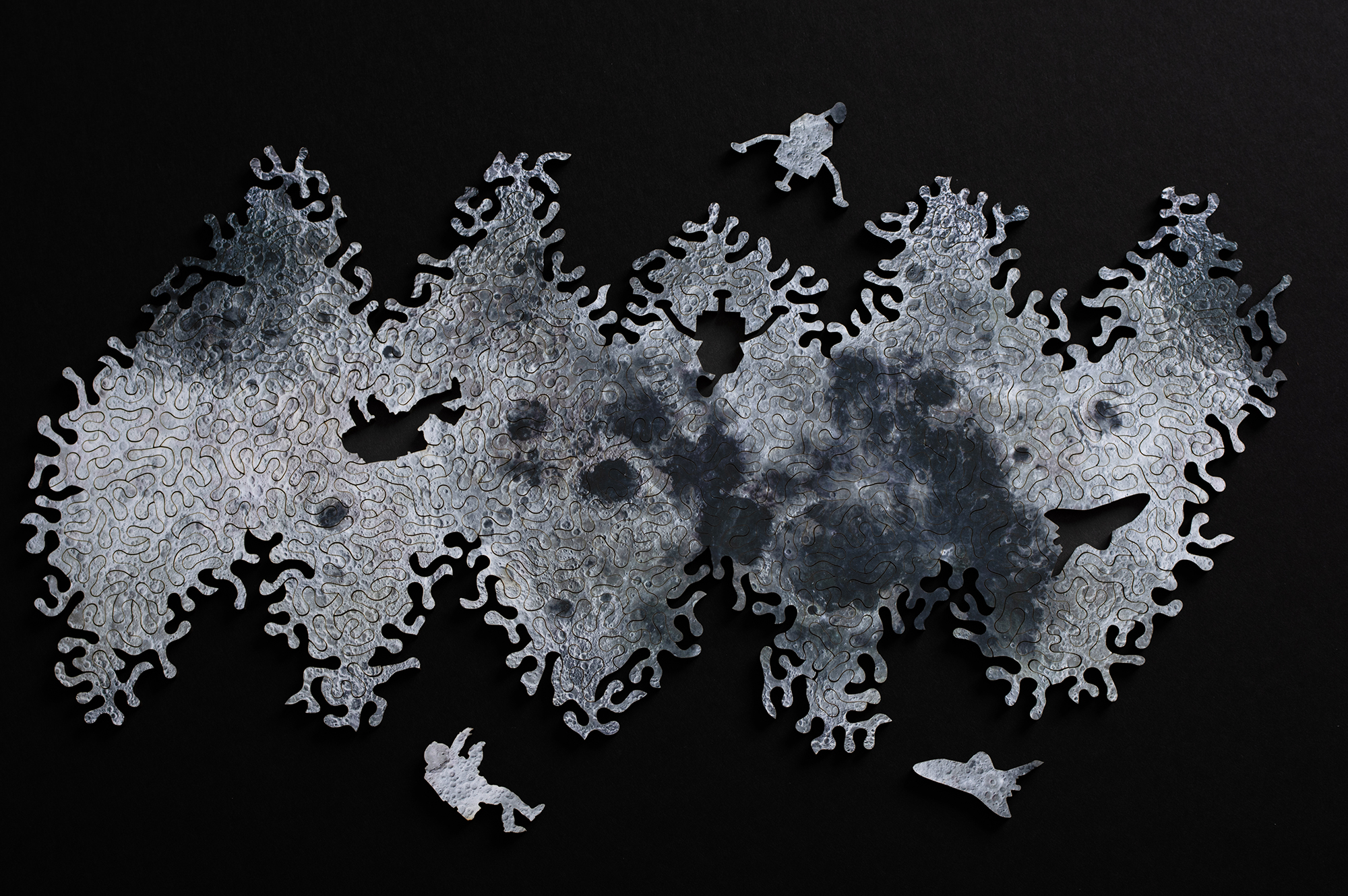
The Earth Infinity Puzzle has 442 pieces and costs $120. As a companion, we are also releasing the Moon Infinity Puzzle so you can also explore lunar geography. The Moon Puzzle has 186 pieces and costs $60. Both puzzles use imagery courtesy of NASA, the Earth from the NASA Earth Observatory and the Moon from the Lunar Reconnaissance Orbiter.

Map Projections

A classic map imposes distortions and orientations that reflect our preconceived notions of the world. The Mercator projection, which is the map we are most familiar with, unrolls the globe into a rectangle with even spacing of latitude and longitude, inflating Greenland into a massive tundra and smearing Antarctica into an unrecognizable white smudge at the bottom. It makes it seem like the Arctic is impassably vast, when actually flying over it is the fastest way to get to Europe from the US. More subtly, it reinforces the idea of a world split into West and East. Even a true globe typically has a fixed North-South axis, forcing us into a certain viewpoint.

The Earth puzzle is based on type of map called a polyhedral projection, where the sphere is projected onto a shape with planar faces and then unfolded flat. In this case, the globe is projected onto a icosahedron, a 20 sided shape of equilateral triangles. This reduces the distortion seen in most maps. This type of map was most famously explored by Buckminster Fuller with his Dymaxion Map. However, unlike the Dymaxion Map, our map is equal-area, meaning the relative size of landmasses is preserved exactly.

We created software to turn a Mercator projection into an icosahedral one. This allowed us to transform photographs from NASA’s Earth Observatory and Lunar Reconnaissance Orbiter into our icosahedral mapping. We use a technique called spherical barycentric coordinates to project the sphere onto the icosahedron. These are area coordinates where every point on a triangle is identified as the weighted sum of its 3 vertices. If you take a point in a triangle and use that to subdivide the triangle into three smaller triangles, then the weight associated with each vertex is proportional to the area of the opposite triangle. Barycentric coordinates are commonly used in computer graphics to interpolate quantities on triangular meshes. You can extend this idea to spheres using spherical triangular patches and their areas. By doing so, the same area on the sphere corresponds to a proportional area on the icosahedron. The whole thing works in a GLSL shader. First we draw a triangle and its barycentric coordinates. We use those coordinates to compute a point on the sphere using spherical barycentric coordinates. From that point, we get the latitude and longitude, which allows us to look up the texture of a Mercator map.

We used the tool to design the projection such that the vertices of the icosahedron do not lay on land. The vertices are the only fixed point of the puzzle, and a seam must pass through them in order to make the puzzle flat. By putting the vertices in the ocean, it means all continents can be assembled into continuous shapes.

Infinity Puzzle

While Fuller always envisioned his Dymaxion Map as reconfigurable, we take this one step further by making a 442 piece puzzle with no edges. There is no fixed orientation or configuration of the puzzle. Assemble it such that all the continents form an almost continuous land mass or put all the oceans together. Put Antarctica in the center. This extends the Infinity Puzzle concept we first introduced with the Infinite Galaxy Puzzle (which has the topology of a Klein Bottle). The Infinity Puzzles are puzzles that truly have no border: pieces wrap around connecting from one part to another. There is no fixed final shape. The first Infinity Puzzles tile, connecting the left to the right and the top to the bottom. The Earth Puzzle’s pieces have more complex relationships, where pieces rotate 60 degrees to zip the seams of the map in different ways. This demonstrates how the infinity puzzles are not simply tiling puzzles but represent a broader range of possible borderless puzzles.

Growing the Puzzle Pieces in 3D

The puzzle pieces we generated for the Earth and Moon puzzles are similar to the maze pieces in our Geode Puzzles. However, there’s a fundamental difference: they had to be grown in 3D on the surface of an icosahedron. To do this, we created a new version of our Maze system which is a simulation of elastic rods. The puzzle piece edges grow, lengthening, until they collide, pushing each other into contorted shapes.  Because the puzzle pieces are growing on a 3D surface, we have to unfold them to a flat pattern so they can be turned into a jigsaw puzzle.

Whimsy Pieces

The Earth Infinity Puzzle includes 16 figure pieces shaped like animals indigenous to different parts of the world: a kiwi on New Zealand, an alpaca in South America, a giraffe and rhino in Africa, and different whales and marine animals throughout the ocean.

The Earth and Moon Infinity Puzzles are for sale in our shop now along with our other Infinity Puzzles.