Corollaria Gyroid is a sculpture created by Nervous System for the Albany International Airport which explores the connections between mathematics and the natural world, highlighting the presence of mathematical principles in biological structures. Measuring almost 7 feet in diameter, it is made up of 121 flat aluminum panels connected by 1789 rivets into an undulating surface perforated by morphing cellular patterns. The surface represented is a gyroid, a minimal surface discovered in 1968 by Alan Schoen at NASA as a purely mathematical invention but which was later found in natural structures such as the scales of butterfly wings. The cellular filigree is inspired by the patterns seen in plant cross sections, bryozoans and the undersides of some mushrooms. The design is generated via a computational system we invented which breaks a surface into flat puzzle piece panels that can be assembled without any forming, jigs or instructions into a complex shape. 

The sculpture will be on display at the airport for the next 3 years in the B terminal where it hangs within a circular skylight. We are so excited to have our work on display at our local airport and also to have been able to realize ideas we’ve been working on for the last several years in metal.

Caption: Photos of the Corollaria Gyroid installed at Albany International Airport. Right photo is courtesy of the Albany International Airport Art & Culture Program

We dedicate this sculpture to the memory of Alan Schoen, who sadly passed this summer. We are grateful to have had to opportunity to meet him and show him our work last year. We hope to carry on his legacy of exploring connections between mathematics and natural world in a playful way.

Caption: Photos of some of the inspirations behind the Corollaria Gyroid sculptures: plant cells, a hexagonal polypore mushroom and bryozoans.

Backstory

We’ve been working on this for over 5 years! Now to be fair, we’ve done a lot of stuff in the meantime, like moved and built a new studio from scratch, released many products, and had 2 children (not to mention the whole pandemic thing), but it’s still gratifying to see something we’ve worked on so long come to fruition.

We started working on the idea of a metal sculpture built out of flat panels in 2018 in a residency at the Autodesk Build Space in Boston. We wrote about our work there previously, which led to a wooden sculpture we created honoring the work of Alan Schoen. However, there were still challenges translating this technique to a stronger, more durable metal sculpture. The basic difficulty is that metal is much harder to manipulate, meaning that lining up panels to attach to each other becomes nearly impossible. 

Panels

Corollaria Gyroid is made up of 121 cell-shaped panels which are elongated along the direction of curvature of the sculpture. 

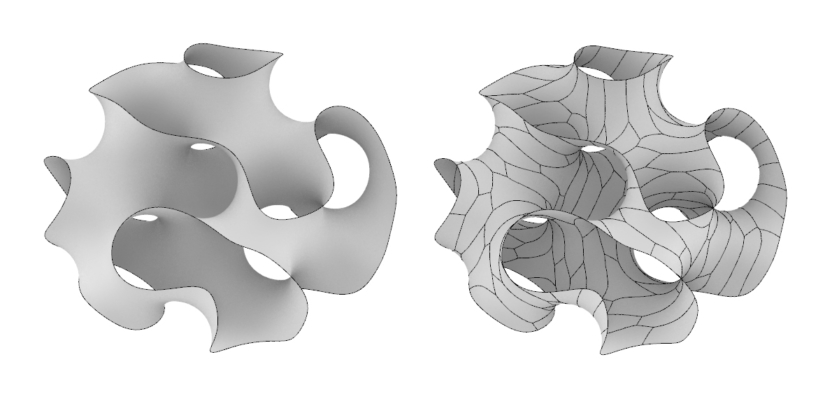
For our previous sculptures, we used Variational Surface Cutting to create the panels. This technique optimizes panel shapes to minimize distortion when flattening, essentially making approximately developable panels. While we like this approach theoretically and the organic shapes it results in, practically it was a failure. Most fundamentally, it tends to make very dissected panels, which, in areas of heavily negative curvature, quickly become self-intersecting when flattened. This is of course, not physically makeable. 

However, a bigger issue is that they are simply difficult to assemble. Because the previous panels are so “squiggly”, it is hard to understand how they need to bend in order to fit together. In wood, you can figure it out as you go, and it can be a bit magical to see it mysteriously all come together. However, in metal you have to apply so much force that you need to know how the panel should bend before you can attach it. These two problems inspired us to take a different approach. Without distinct seams in the surface, what variational surface cutting basically does is make panels thinner. The closer the surface is to the edge of a panel, the easier it is to flatten. So we asked what if we just made panels that elongated in one direction to make them thinner? If they are basically straight, they will never intersect themselves when flattened. If we choose that direction of elongation to also be the direction of maximum curvature, then the panel shape itself tells us how it needs to bend.

Patterning

Caption: Detail of Yellow Moon Gyroid (2022) vs. Corollaria Gyroid (2023)

The sculpture features a continuous pattern of cells which shift in scale, direction and size across the surface. This approach to patterning differs both aesthetically and functionally from our previous works. The panels of Yellow Moon Gyroid have a solid border to accentuate their sinuous figure which evokes “pavement” cells in leaves. With our changing panel strategy, we switched to a globally continuous pattern which seamlessly crosses panels, causing them to disappear in the design.

This additionally contributes to the ease of assembly. To illustrate this, think of trying to approximate a sphere with a small circular panel. If you have a solid border, your panel can only bend into a U shaped circle without stretching. Your error is roughly proportional to the size of your panel. However if the border is eroded away into just a cross touching the border in four places, you can now bend each arm to approximate a hemisphere with 4 holes in it. Now your error is proportionally only to the thickness of your pattern. By having our panel edge dissected, it makes it easier to conform to the complex curvature of the sculpture without deforming the material in some kind of forming process.

Technique

The design of both the panels and the pattern uses surface based anisotropic centroidal Voronoi optimization. That’s a lot of technical terms so let’s break it down. A centroidal Voronoi diagram is a set of cells where their centers are also their centroids. Essentially it’s distributing cells as evenly as possible, which has a lot of nice properties. Saying it’s anisotropic means those cells are non-uniform; they can have different sizes and shapes. We can control those sizes and shapes with a metric, which specifies how the cells morph and stretch throughout space. We have made heavy use of anisotropic centroidal Voronoi diagrams in our previous work for 2D shapes, like our Corollaria railing. For the sculpture however, we need to do it on a complex surface.

The switch from 2D to 3D or surface embedded cells requires a change of perspective. In 2D, in order to make our cells anisotropic, what we do is change our definition of distance. Normally the distance between two points is defined as . This creates a unit circle around a point of all points that are a distance 1 away. If we introduce a metric , a matrix defining a scaling and rotation, and define distance as , we get an ellipse. Using this new definition of distance to calculate our Voronoi diagram and centroids gives us the anisotropic control over our designs.

However, doing this in 3D or on a surface, either analytically or through approximation becomes computationally difficult. However, we can take a different approach. Rather than thinking about changing how we compute distances, we can think about it as changing the shape of space. We can distort space using the same metric we used to distort distances, and then just compute regular old distances. To be more concrete, we input a mesh, stretch out all the triangles of that mesh however we want, compute a Voronoi diagram on the stretched out shape, and then map that back to our original shape.

We’ve done this before with our work on 3D-printed organs in 2018. We designed an alveoli analog by creating cells that stretch in the direction of fluid flow. This technique has a problem though. If you just stretch out your surface in 3D arbitrarily, most of the time, you’ll end up with a surface that self-intersects, rendering your distance calculations meaningless. To avoid this you can instead embed your surface in a higher dimensional space. By adding more dimensions, there’s a lot more room to deform your surface without bumping into itself. We created an implementation of this idea based on the paper “Computing a high-dimensional euclidean embedding from an arbitrary smooth riemannian metric” by Zhong et al.

Both the panel and the pattern are computed in 8 dimensional space and then projected back down into 3D space. For the panels, our metric is defined by stretching in the direction of maximal curvature. For the pattern, we design a custom metric to give a sense of dynamism to the piece, where the cells are reminiscent of bryozoans.

The pattern is then broken up into pieces by which panel it lays on. Those pieces are thickened on the surface and then conformally flattened using Boundary First Flattening by Keenan Crane. This gives us a flat version of the panels with minimal distortion where the length of the boundary is preserved. We finally add holes where corresponding panels connect and labels to guide assembly for our fabrication drawings.

Our software makes use of Nick Sharp’s geometry central, for computing direction fields and flattening, and Bruno Levy’s geogram for computing surface intersections and high-dimensional centroidal Voronoi diagrams.